Supertangrams

Many years ago, in the exhibits area at an NCTM national meeting (in New Orleans?), I saw math teachers standing in an insanely long line. I had never seen anything like it, and never saw anything like it since. They were waiting to have a book signed by Martin Gardner, the author of the “Mathematical Games” column in Scientific American, and of the many books where those are collected. I was not surprised to see he was a hero to so many of my colleagues: it may well be that this one man did more to steer people into our profession than anyone else! 

Ted Hertz, my late father-in-law, was a computer engineer in the early days of electronic computing. He had a great interest in recreational math. He introduced me to Martin Gardner, and in particular to pentominoes, the shapes consisting of five unit squares joined edge-to-edge. Those were a recurring topic in Gardner’s writing, and the source of many, many puzzles. I started playing around with those, including for example a search for Simultaneous Pentomino Rectangles. Ted helped me by writing computer programs to confirm and expand my discoveries. 

Pretty soon, I started thinking about how to use pentomino puzzles in the classroom.  The key was to remove the requirement that all puzzles use the full set of 12 pentominoes. I created dozens of pentomino puzzles, which turned out to be very popular with students, and ended up in my first published books. (You can download those here.)

In 2013, Didax published my Working with Pentominoes, a book of puzzle-based lessons. Read more about pentominoes in Geometric Puzzles in the Classroom, and find many pentomino links on my Geometric Puzzles home page.

Supertangrams

In many ways, pentominoes were a great success story for me: they launched my career as a curriculum developer. Encouraged by this experience, I started exploring what is the main topic of today’s post: supertangrams. Supertangrams are the shapes made by joining four isosceles right triangles (each one half a unit square) edge-to-edge. Because they share much of their geometry with the well-known tangrams, and in fact include all three tangram shapes, I named them supertangrams. 

Here they are:

Creative Publications published two books of supertangram puzzles, in the style of my pentomino books (Supertangram Activities 1 and 2). However, unlike my pentomino puzzles which can be used with pretty much anyone, it turned out that supertangram puzzles were, well, super-hard. So I followed up with SuperTangrams for Beginners, 1 and 2, hoping that those could serve as a training ground to prepare kids for the other books.

Long story short: supertangrams were not a commercial hit. The publisher put them out of print, and sent me the remaining copies of SuperTangrams for Beginners 2 — perhaps two or three hundred books. They are still sitting on a high shelf in my office.

When the books went out of print, I asked the publisher for information on the manufacturer of the plastic supertangrams they had been selling. I figured I should have a couple hundred sets while I searched for another publisher. I contacted the manufacturer, and asked how much it would cost me to purchase that many sets. Instead of a reply, I received gigantic boxes filled with thousands of supertangram sets. Those have been sitting in my basement ever since. I’ve been selling a handful every year, almost exclusively to teachers who had been using supertangrams with their students, but had no place else to go to get more as pieces got lost.

That they were not a commercial hit does not mean they are not great! I created some supertangram materials to use in my geometry classes, and posted them on my website. I also shared those activities whenever I offered my Hands-On Geometry summer workshop, and often as part of my puzzle-oriented presentations at conferences. 

The Grid

The reason supertangram puzzles can be difficult is intrinsic to the shapes. In a pentomino puzzle, you know that the piece’s edges will be parallel (and perpendicular) to the puzzle edges:

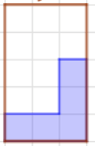
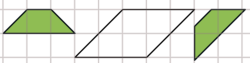
In contrast, in a supertangram puzzle, things are more complicated:

In this example, it is clear that the trapezoid should be placed with its longest side along the bottom of the parallelogram, because placing it the other way clearly doesn’t fit. However in a larger puzzle it would not at all be as obvious. Placing pieces in a way that does not match the underlying grid is fatal. To help solvers understand that, I showed the grid in most of the puzzles in SuperTangrams for Beginners 2. For example in this case seeing the grid helps to orient the trapezoid:

The visible grid is a big help, and after solving enough puzzles where it is shown, you develop a familiarity with the shapes, and become able to deduce the puzzle’s orientation even if the grid is not shown.

A few weeks ago, I got interested in some puzzles which were missing in the existing supertangram books. Some I had known about, and some I created from scratch. I solved them, and assembled them in a (virtual) book which I added to the existing Supertangram Books page. In addition to the unit mentioned above, you now have access to five free supertangram books.

Discounter Introduces Reductions!

It’s time I share supertangrams with a broader audience. I realize they are not going to be the sort of hit I had with pentominoes, but I should make more of an effort to get them out there. So I’m drastically lowering the price: until August 22, I will sell them to you for $2 per set, plus $10 for shipping and handling. And if you order four or more sets, I’ll include a free hard copy of SuperTangrams for Beginners 2 while they last. 

End of sale: Starting on August 23, 2023, the cost is $3 per set, plus $12 for shipping and handling. Click here for more information!

— Henri