Asilomar Report: Conic Sections

As my retirement starts to kick in, I no longer attend conferences — except for one: the annual meeting of the California Math Council (Northern Section.) Once again, I had a great day at Asilomar, a beautiful spot near Monterey, right on the Pacific Ocean. Here is my annual report.

Conic Sections

Figuring out an approach to any substantial topic takes time and effort, and that is rarely shared publicly. Nolan Fossum’s presentation is the sort of session I’d love to see more of at conferences. He shared his current approach to teaching conic sections — as a work in progress. His goal is to have less memorization, less reliance on formulas, and more intellectual engagement from his students. As a participant, I really appreciated being invited into his process. (He frequently acknowledged his approach needs work, and he encouraged us to send him our suggestions.)

I will not try to summarize the whole talk, instead, I’ll focus on one wonderful thing I learned. Let me set the stage for it.

In the construction unit I created for my geometry class many years ago, I challenged students to construct points equidistant from a point F and a line d. One such point (V) is easy to find after dropping a perpendicular from F to d: 

Soon after that, students realize that drawing a parallel to d through F helps to find points A and B, equidistant from F and d:

This is correct, as A, F, and D are three vertices of a square, and likewise B, F, and D.

At that point, I tell students  that there are many more points equidistant from F and d. If necessary, I suggest that choosing a point T on d may be helpful. Where are points that are equidistant from F and T? How does that help us? This leads to the construction of a generic point P, which is equidistant from F and d:

The locus of P as T moves on d is the parabola with focus F and directrix d. (That, of course, is the geometric definition of the parabola. Read more about this here, and here.)

(Here is the GeoGebra file I used to make the above figures.)

Back to Nolan’s talk. He calls points A and B the “anchor points” for the parabola, and he asks: what is the slope of VB? I had never thought about this. If you are familiar with the construction of V and B (as in the second figure above), it is easy to figure out, and it is the same for all parabolas! Once you know this and the coordinates of the vertex, you have a way to find the coordinates of one of the anchor points. This in turn means that if you know the coordinates of the vertex, you have a straightforward way to locate the focus and the directrix without a lot of memorizing. I love this!

There are other geometric constructions of the parabola, of course, but this one is particularly important because it throws light (heh) on the parabola’s reflection property. (Again, see this page on my website.)

This very same construction came up later in the day. Along with many others, I tried to attend another talk on conic sections. Here is an excerpt of the session’s description:

…construct conic sections as the curve of symmetry between a circle and a point inside the circle, an infinitely large circle and a point, and a circle and a point outside the circle, revealing how the ellipse, parabola and hyperbola
relate to each other.

The presenter never showed up, but a few of us stuck around, and tried to make sense of this. I had never heard the phrase “the curve of symmetry”, but I like it. I realized that the “infinitely large circle” mentioned in the summary is line d in the above construction. That led me to see that by following the same steps I outlined above, but putting F inside (or outside) a circle d, we should be able to create an ellipse (or hyperbola.) It was very satisfying to use GeoGebra to see that indeed this worked, and even more so to prove this was correct. Here is the figure I made:

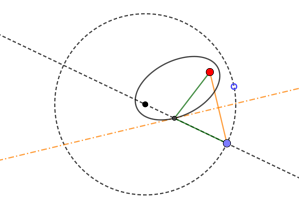
See if you can prove that the curve is indeed an ellipse. (Where are the foci?) Dragging the red point outside, it turns into a hyperbola. The proof is similar.

(Here is the GeoGebra file.)

In other news…

I co-presented “Lessons from Lew” with Kim Seashore. (Read more about Lew Douglas here. Get all the handouts, plus other relevant materials here.) As is usually the case when presenting something for the second time, it went really well. I was really pleased at the participants’ creativity in the kinesthetic part of the session: they came up with excellent representations of 60° angles, complementary angles, etc… Later, when discussing the Symmetric Polygons handout, Dan Bennett astutely noted that we used “at least two lines of symmetry” for the equilateral triangle, but did not try for a formulation with fewer than four lines of symmetry for the square. (This could have been “at least three lines of symmetry”, or “at least one line of symmetry through vertices, and one line of symmetry not through vertices”.) Logically, he has a point, but he agreed that pedagogically this was probably the right call.

Later, I presented “Connect the Dots”, which was a combination of curricular lessons and assorted puzzles using the geoboard (or dot paper.) I have presented the curricular part many, many times, and it always goes well. More recently, I ran some Math Teachers’ Circles focusing on teacher-level challenges. Combining all that into one talk turned out to be a great idea. Kate Philpott pointed out that the puzzles I intended for teachers could work as extensions for students, even in fifth grade. Of course she’s right. Including those puzzles helped to make the session relevant to ages 9 to 99 — as advertised.

So yes, I had a great day. Alas, I didn’t get to take my usual walk along the coast, so I’m already thinking about what I should present next year. Whatever it is, I’ll be sure to take that walk!

— Henri