Virtual Manipulatives: Part 2

In the previous post, I discussed virtual manipulatives in general, and a particular implementation for algebra, using a Google Drawings representation of the Lab Gear. In this post, I will explore GeoGebra as a platform for virtual manipulatives.

Pattern Blocks

Virtual pattern blocks are not hard to find on the Web. One good implementation is on the Math Learning Center site. Among other valuable features, it allows the selection of a group of blocks which you can copy-paste, for example in creating a pattern block tiling. One inexplicable choice was the inclusion of a purple isosceles right triangle. This makes no sense to me because its hypotenuse will not match the sides of any of the actual pattern blocks. (On the other hand, one good use of this purple block would be to discover the supertangrams, but there’s no reason to include it in the same applet as the pattern blocks.)

I was interested in creating more specialized pattern block applets, which would focus on specific activities. My first creation along these lines is to support Lab 5.6 from Geometry Labs. The lab is an exploration of symmetry, in which students cover three figures with pattern blocks. I started with Jen Silverman’s GeoGebra pattern blocks, and added the figures. This is what it looks like:

(Check out the applet.)

The beauty of virtual manipulatives in GeoGebra is that you have access to the full power of the software. For example, I used the rotation tool to make this figure:

And this one, using reflection across just two mirrors, executed repeatedly:

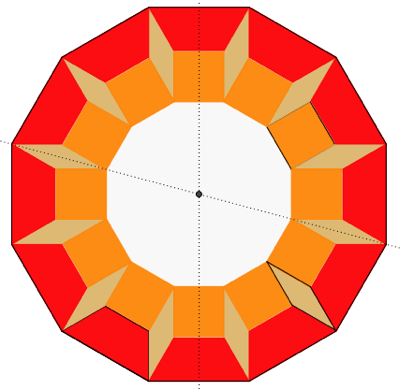
(Look at more double-sized pattern block dodecagons on my website.)

However, the limitation of GeoGebra for virtual manipulatives is that it’s inconvenient and complicated to create multiple copies of blocks, which is of course necessary for pattern blocks. The existing GeoGebra Rigid Polygon tool has the potential to solve this problem. The tool duplicates any existing polygon by simply clicking on it, and the copy can be rotated “manually” by dragging one of the vertices around another. This could be used to create as many copies of the original pattern block as you want! The problem at the time of this writing is that the copies do not inherit the properties of the original: the colors, styles, and scripts are lost. If that was fixed, GeoGebra would be a terrific environment for virtual pattern blocks (and any virtual manipulatives used for tiling.)

More GeoGebra Manipulatives

Tangrams

Multiple copies is not an issue for tangrams, and I was able to create a decent GeoGebra Virtual Tangrams applet.

This applet will work for the tangram activities in Geometry Labs, or really any tangram activities, but it does not add anything to what you can do with more enjoyment using physical tangrams. I expect that a similar approach will work for other geometric puzzles, such as pentominoes and supertangrams. However those will take more work due to the greater number of pieces, so I have not yet embarked on those projects. [See my update below!]

Geoboard and Similar

There are a number of online geoboards, some of them beautiful. The best of the lot is the one on the Didax site, which makes it possible to do all the geoboard activities in Geometry Labs. It looks like a physical board, includes rubber bands in five colors, and unlike most of the others, it has the 11 by 11 dimensions needed for the Geometry Labs. And it even has a circle geoboard version. Still, I decided to make my own GeoGebra Virtual Geoboard and Virtual Circle Geoboard.

They do not try to look like physical geoboards. Instead, they make it possible for a tablet user to handwrite or draw directly on the board, not unlike what one might do on a whiteboard, except that the figures are extremely accurate. Here are two examples:

(Check out the applet.)

(Check out the applet.)

Also note that the inside of polygons can be colored, a possibly useful feature that is not available on most online geoboards.

Along the same lines, I made some Virtual Grid Paper — not exactly a manipulative, and not an electronic graphing utility, but useful in doing all sorts of math. 

(Check out the applet.)

Conclusions

1. The main purpose of manipulatives is to enhance classroom discourse. Virtual manipulatives are not as effective for that as the physical kind, and should not merely imitate those. Rather, they should take advantage of the power of the computer to enrich the experience.
2. To avoid some common design mistakes, virtual manipulatives should be created in consultation with educators who understand how they might be used in the classroom. Or, they could be created by the educators themselves. This has become more possible thanks to platforms such as Google Drawings and GeoGebra. Each platform has its shortcomings, but they do allow an amateur like myself to create useful learning environments, closely tied to curricular materials. I link to all my virtual manipulatives here.
3. Google Drawings allow the manipulation of virtual objects in a way that is vastly more accessible than traditional graphics software. Figures can be annotated with (typed) text. Multiple students can interact with the figures simultaneously, in a way that could promote collaboration.
4. GeoGebra is of course full of tools of every sort, some of which can profitably be included in a virtual manipulatives applet. In this post, I mentioned the geometric transformation tools, the availability of “snapping” to a grid for accuracy, and the possibility of handwriting right on the figure.

Many online manipulatives are pale imitations of the real thing. Some are well-thought-out imitations of the real thing. And some are in some respects superior to the real thing. In this post, I tried to suggest some ways to move in the direction of the third category.

Addendum

I used GeoGebra to make Virtual Pentominoes. Read on to see suggested sample lessons.

Adjust the rectangle to the desired size, and solve the puzzle:

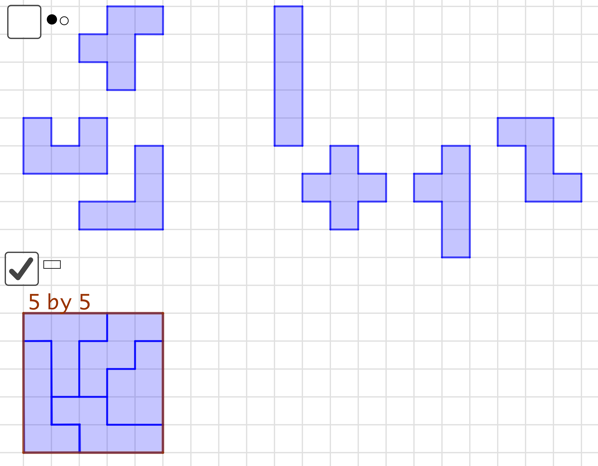
What rectangles are possible?

Or, hide the rectangle and use the Polygon tool to create your own puzzle, for example by doubling or tripling pentomino dimensions:

(The two types of visible vertices are how you turn and flip the pieces.) Now solve the puzzle, and hide the vertices:

(Check out the applet.)

In this example, we doubled the dimensions. What happened to the area? What would happen if we tripled the dimensions? Which puzzles of this type can be solved?