I had the good fortune of mentoring Liz Caffrey for five years, at the very beginning of her teaching career, when she worked at the high school where I chaired the math department. She is now a veteran and talented middle school teacher in the Boston area, but we’ve stayed in touch. In this guest post, she shares how she uses the Lab Gear with her 7th and 8th graders.
There is a massive amount of information about the Lab Gear on my website. I will insert some relevant links and comments in the body of Liz’s post, [in square brackets]. To purchase Lab Gear materials, go to Didax.
— Henri
Lab Gear in Middle School – The Great Connector
By Liz Caffrey
Before I started teaching, I always saw math as a means to an end, that end being physics. But one semester teaching Geometry with Henri, and I was converted. I saw that math was, in and of itself, a beautiful discipline. And now I see it as my job to show that side of math to my students.
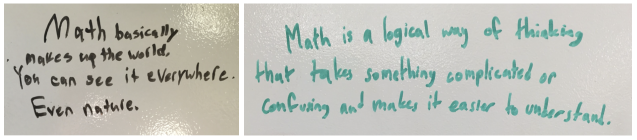Definitions of math, written by two of my eighth graders on the first day of school.
I teach sixth through eighth grade at a middle school I helped start, which has been a dream come true. In planning to teach middle school, I adapted a lot of the techniques I learned when working with Henri. One thing I brought with me has been the Lab Gear. Those manipulatives have been an invaluable tool to bridge the gap between the concrete world of numbers and the abstract world of variables. Lab Gear also helps students see the deep connection between algebra and geometry. And, perhaps most importantly, Lab Gear provides both access for struggling students and big challenges for students who want to go deeper.
In my first year of teaching at my current school, I bought flat algebra tiles (the ones that have different colors for negative and positive) rather than Lab Gear. I did this, frankly, to save money. However, I found that it was not worth the savings. First of all, I had to adapt all of Henri’s stellar curriculum for different manipulatives, which was time-consuming. Second, there was something less satisfying for my students about manipulating the tiles; I think it had to do with the fact that they are flat, unlike the Lab Gear. And third, the lack of 3D challenges meant that I was not able to differentiate the lessons as much. Most importantly, the connection between algebra and geometry was not as strong in students’ minds. After that first year, I invested in a class set of Lab Gear and never regretted it.
Students comparing their simplified polynomial expressions for a collection of Lab Gear blocks
built for them by a classmate.
My middle school students first encounter Lab Gear in the winter of seventh grade, right in the middle of middle school. By that point, my students have seen variables when they derived formulas for area and volume in sixth grade. In the Fall of seventh grade, we do a lot of Visual Patterns, where they derive algebraic formulas to describe a shape at the xth step of its growth. This routine gets students itching to know how to simplify algebra expressions, since they want to prove that their different formulas are equivalent!
[Note: each Lab Gear book includes a few problems in the Visual Patterns format.]
Once students familiarize themselves with the Lab Gear blocks’ names, one of the first things we do is build the xth step of the pool border problem with Lab Gear, first with a square pool, and later with a general rectangle. This provides a nice connection for them to what they have already experienced with algebra. It also provides a goal for us – by the end of the unit, we should be able to simplify all of these expressions!
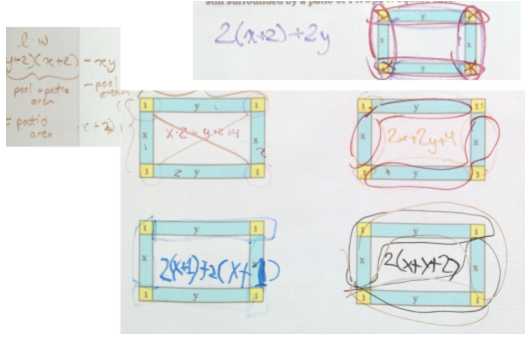Five ways of expressing the 1 by 1 border of an x by y pool, by seventh graders.
[This is a creative use of the Lab Gear, which I had not thought of!
You can find a version of this problem in Algebra: Themes, Tools, Concepts: Lesson 7.2 Square Windows, and a three-dimensional version in Thinking/Writing 7.A Cube Problems. The latter could also be modeled with the Lab Gear.]
Next we work on naming polynomials, which is how students learn the basics of combining like terms. The blocks clearly communicate the concrete idea that the coefficient (the number of blocks) can change but not the variables or exponents (the name of the blocks). This is a crucial concept that we keep coming back to.
Students leaning in, comparing answers on a Naming Polynomials activity.
Next we work on perimeter and surface area challenges. These activities have the dual purpose of providing review of combining like terms for students who need it and adding layers of challenge for those who are ready for it. For example, subtraction of terms arises from two unequal blocks being laid against another, yielding terms for side lengths such as y – (x + 2) that need to be simplified and then added to all of the other sides.
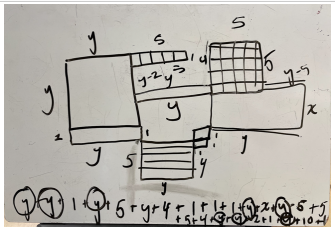Student work, attempting to simplify a Lab Gear perimeter problem created by a classmate.
I always make time for students to build their own Lab Gear perimeter and surface area challenges. Their creations are far beyond the challenges of the activities from the Lab Gear books. I have students solve their own and each other’s challenges as a check.
Pieces of Lab Gear “furniture” built by students in a make-your-own Surface Area challenge activity.
[The perimeter and surface area problems are among my favorites in the entire Lab Gear universe. (Thus, there are some such problems in all the Lab Gear books.) I have not had students make up their own challenges, and I am blown away by the creativity and complexity of Liz’s students’ creations!]
Next we take a break from simplifying expressions to work on solving equations. Starting with Which is Greater? drives home the idea of equality versus inequality between two expressions. The use of the minus area and the simplicity of the line between equal expressions allows students to see how beneficial it is to simplify each expression before operating on both sides. The idea of doing the same operation to both sides is so clear and concrete with the workmat. It starts with subtracting the same piece from both sides (that preserves the balance) and then moves to more nuanced ideas such as adding the opposite and dividing both sides by a number. All of this is scaffolded beautifully with the Lab Gear activities.
Solving an equation with Lab Gear and algebra simultaneously, with conclusions of what “legal moves” are allowed when solving.
(The green line of math is the check step, which we did at the end.)
The last algebra concept that we cover in seventh grade is the distributive property. The “Make a Rectangle” and “Make a Box” Lab Gear activities reinforce the “box method” that my students learn for two-digit multiplication in elementary school. For this reason, this part goes quickly, and they “graduate” from Lab Gear to boxes on paper quite quickly. We revisit the box from the inside to the outside when we factor polynomials in eighth grade. Kids need a quick reminder of how the blocks work and then they are just fine. I love to do it for completing the square too, when we have enough time to get through that topic at the end of 8th grade.
Two students simplify (x+2)(x+3), one with Lab Gear, and the other by drawing the area model.
From day one, the question “do we have to build it?” comes up. I always leave it up to the students as to whether they are ready to wean off of the Lab Gear, but should a dispute or question arise, we always return to the blocks to build it and see how the geometry can help us understand the algebra. Just as I always allow students not to build, I always allow students to build, including using Lab Gear on quizzes.
Students pairing up to add and subtract polynomials without Lab Gear, near the end of the unit.
Henri’s penchant for puzzling really comes through in all of the Lab Gear activities. Challenges like “find as many Lab Gear arrangements that produce a perimeter of 2x + 4y” sparks so much creativity, collaboration, and discussion amongst my students. It also drives home the idea that “there is no one way” (another Henri-ism). Later on, the rectangle puzzles are so fun and engaging, kids do not even realize that they are factoring quadratic trinomials!
Lab Gear truly is the great connector in my math classroom. It connects geometry and algebra, concrete and abstract, access and challenge. Moreover, it connects students to one another as they grapple together and push one another to tackle complex-looking expressions made meaningful through tangible representation in the physical world.
[Thanks, Liz!
Liz will be hosting a workshop for math instructors, titled “Building a Culture of Collaboration” at the Atrium School in Watertown, MA, July 19-21. More information.
For more information about the Lab Gear, go to my website, or ask your questions in the comments below.
— Henri]
Henri's Math Education Blog 