Wallpaper Symmetry Part I

While sheltering in place, I decided to use some of my time to complete a project I had been contemplating for a long time: creating a catalog of the 17 wallpaper groups using pattern blocks. It is now live on my website: Wallpapers Catalog. The idea is to provide a bridge between schools, where pattern blocks are ubiquitous, and pure math wherein a theorem states that from the point of view of symmetry, there are only seventeen possible wallpaper patterns. When I used these words in an online conversation with artist Nora Rodriguez, this is how she pictured “the point of view of symmetry”:

In this post, I hope to explain what I meant. This is not going to be an exhaustive analysis of the wallpaper groups, only a clarification of what we mean when we say that mathematically, there are only 17 possibilities. (Of course from other points of view, the possibilities are infinite!) I will not discuss this from the point of view of abstract algebra: my approach will be visual and geometric.

Analyzing the Symmetries of a Tiling

We’ll start with an example. Many bathroom floors are tiled with regular hexagons, like this:

(In the rest of this discussion, you must imagine that the tiling extends infinitely in all directions.)

Let us analyze this design’s symmetries. First of all, imagine a line that joins opposite vertices of one of the hexagons, like this:

This is a line of reflection for the (infinite) tiling, a mirror line. Can you see how each hexagon, or half-hexagon is reflected on the opposite side? The same is true of all such lines:

(I did not draw all of them — again, you have to use your imagination to complete the picture.) Reflections in these mirror lines are among this tiling’s symmetries.

But there are more mirror lines: the ones we would get by joining the midpoints of opposite sides of the hexagons:

Reflections across those lines are also part of this tiling’s symmetries. The next figure shows both sets of mirror lines:

There are no other mirror lines, but there are more symmetries: rotation symmetries. A figure is rotationally symmetric if after turning it less than a full 360° around a center, it appears unchanged. Our hexagon tiling has three types of rotation symmetry: 2-fold (180°), 3-fold (120°), and 6-fold (60°). The figure shows the centers of symmetry, color-coded:

If you turn the whole plane 180° around one of the red centers, the figure will appear unchanged. Around the green centers, you can turn 120° or 240°. And around the blue centers, 60°, 120°, 180°, 240°, or 300°. These rotations are also among the tiling’s symmetries.

All of the symmetries are represented together in this figure:

Analyzing More Tilings

Now let’s analyze this tiling:

The tiling is more complicated, but as you will see it has exactly the same symmetries:

• Mirrors between adjacent blue tiles
• Mirrors joining opposite points of the six-pointed stars
• 2-fold rotation centers at the common vertices of hexagons
• 3-fold rotation centers at the centers of the hexagons
• 6-fold rotation centers at the centers of the stars

Here is a figure showing all the symmetries:

And here are the lines and centers of symmetry, without the distraction of the tilings where we found those:

The second image is more spread out, but notice how they have the same structure. Each blue dot is surrounded by alternating red and green dots forming a hexagon. Each green dot is surrounded by alternating red and blue dots, forming a triangle. Each red dot is surrounded by alternating blue and green dot, forming a rhombus. Some lines go through red and green dots alternately, while others follow a green-red-green-blue pattern. 

In other words, from the point of view of symmetry, the two tilings are equivalent, even though they are quite different on the surface. Here are two more pattern block tilings that share exactly the same structure. Can you find the mirror lines? the centers of rotation? Can you confirm that the mirrors and centers are arranged, again, in exactly the same way?

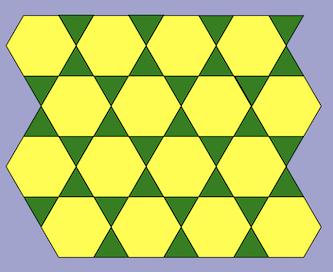
(The latter image was contributed by John Golden. Be careful: not all the hexagons have the same job in his tiling!)

Crystallographers call this symmetry pattern p6mm. It is one of the seventeen possible wallpaper patterns. From the point of view of symmetry, all four tilings above share the same structure: mirror lines and centers of rotation are organized in exactly the same way. This is not a coincidence! In my next post, using this pattern as an example, I’ll try to explain why wallpaper patterns are so constrained.

— Henri

PS: For the purpose of this post, I made my tilings using the Ontario Ministry of Education applet. (I added the mirror lines, the rotation centers, and the legend using Affinity Designer.)  John made his tiling using the Math Learning Center applet.