This post is a continuation of Wallpaper Symmetry Part 1, which you should read first. Both posts are companions to the Wallpapers Catalog on my website.
———————————————————————
A long time ago, in my twenties, I attended a lecture about the mathematics of wallpaper designs. The presenter gave an overview of the entire proof that there are only 17 different wallpaper groups. (Groups are mathematical structures which are foundational to symmetry, to the Rubik’s Cube, and to the number systems we use every day. Learn more about this in my Abstract Algebra unit.) I probably did not follow the whole argument then, and I certainly don’t remember it now. Still I have no trouble believing that from the point of view of symmetry, there are only 17 possibilities for an infinite repeating two-dimensional design (a wallpaper).
In this post, I will try to get across some reasons why possibilities are so constrained. In the last post, I analyzed wallpaper designs that include both six-fold rotations and mirror lines, and showed that several such designs have exactly the same structure. Today I will show that given that assumption, no other structure is even possible: if a repeating design includes a mirror and a six-fold rotation center, then it must be structurally identical to the designs we analyzed in the previous post.
The argument I will make will be visual and geometric, and even though it will not be 100% rigorous, it should be sufficient to convince you that the mathematical choices for a wallpaper design are quite limited.
Preliminary Results
We will need some basic facts to help us navigate this argument.
Fact 1: If two mirror lines intersect, their point of intersection is a center of rotational symmetry.
For example, if two mirror lines are perpendicular, then an item such as the shape labeled 1 in the figure is reflected as shape 2 in one mirror. Shape 2 is reflected as shape 3 in the other mirror. Shape 3 is reflected as shape 4. The overall result is 2-fold rotational symmetry, centered at the intersection of the lines.

If the lines make a 60° angle with each other, we can follow the reflections alternately in a similar way, leading to three-fold rotational symmetry:

If the lines make a 30° angle with each other, we get six-fold rotational symmetry:

We will encounter all three of these situations below.
(You can and should try this experiment yourself using GeoGebra or any interactive geometry software: start with two intersecting lines, and see what happens when you reflect an asymmetric shape repeatedly, alternating between the two lines. Depending on the angle between the lines, you will get more or less interesting results. What angles yield the most visually pleasing results? It is also worthwhile to carry out the same process with two parallel lines, or three lines that make an equilateral triangle, etc.)
Fact 2: The reflection of a mirror is a mirror.
This is because if a line is a mirror line, the whole design is reflected in it. Here is an example based on the above figure:

The new lines were all created by reflecting the original mirror lines in each other, and the resulting lines in each other, and so on. All of them are indeed mirrors. Those symmetries were already in the figure, a consequence of having the original two mirrors.
Similarly, the reflection of a center of n-fold rotation across a mirror line is a center of n-fold rotation. The image of a mirror in a rotation by the appropriate angle around a center of rotational symmetry is a mirror. The image of a center of n-fold rotational symmetry in a rotation by the appropriate angle around a center of rotational symmetry is a center of n-fold rotational symmetry. A concise way to put all this: symmetries propagate each other.
The Argument
We are now ready to see why if we have six-fold rotational symmetry and a mirror line in a repeating design, then we must have the entire structure we explored in the previous post.
First, let us assume that our center of symmetry is not on our mirror line, like this:

Because symmetries propagate each other, there must be another six-fold center on the other side of the line:

For the same reason, there must be a mirror that is the result of rotating our original mirror 60° around that center:

That mirror goes through our original center. (This is not an accident. I won’t do it here, but it can be proved using basic high school geometry.) But since we have six-fold symmetry, rotating this new mirror 30° around our original center gives us a new mirror:

Our new mirror passes through our second center.
Let’s now show all the mirrors through our two points:
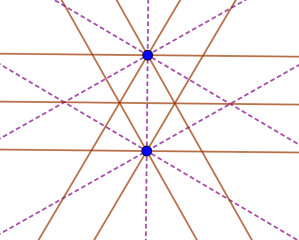
(I color-coded the points and the mirrors more or less with the colors I used in the previous post.)
But look at all these mirror intersections! As we saw above (Fact 1) these are all centers of rotational symmetry. If the angle is 90°, two-fold. If 60°, three-fold. If 30°, six-fold:

As you see, this is exactly the pattern we saw in the previous post. Perhaps it will be more obvious if I show a little bit of the hexagon tiling that got us started:

Conclusion
What I tried to show is that from the point of view of symmetry, there is only one way for a wallpaper pattern to have both six-fold rotational symmetry and mirror symmetry. Starting with a single mirror and center, plus some math facts, we found that the pattern had to include a whole network of mirrors and centers, including some two-fold and three-fold centers, all of them organized in the pattern known as p6mm by crystallographers.
(I started the argument with the original center off the original mirror. A very similar argument would work if our original center was on the original mirror.)
I hope I convinced you that the options for symmetry in two dimensions are severely constrained. Not everything goes!
For further exploration, visit the pattern blocks Wallpapers Catalog on my website.
— Henri