Tiling and Transformations

In my last post, I argued that tiling is a good topic to include in a geometry program. Students find it engaging: on the one hand, it connects with art and culture; on the other hand, it provides a context for student creativity. At the same time, it presents many connections with the geometry curriculum in middle school and high school.

In this post, I will elaborate on one curricular connection: the basics of transformational geometry, including recognizing the four types of isometries, and some theorems about composition. To illustrate my points, I will use some examples, but the same ideas can (and should) be explored in periodic tilings created by students, or ones they (or you) find in the world or online.

Using this context is one way to counterbalance the terribly disappointing approach that dominates so many curricular materials on transformations. Those often begin on the Cartesian plane, and prioritize algebra (what happens, e.g. if we add 3 to the x-coordinate and 4 to the y-coordinate?) Moreover, they act as if the only reflections are in the x- or y-axis, and the only rotations are 180° around the origin. Using tiling as a context for the introduction of isometries is one way to anchor them in a visual and geometric domain. This makes them more interesting, more accessible, and more mathematically rich.

[For a complementary approach to what I share in this post, see some of the materials I developed to introduce the isometries and dilation, on my Geometric Transformations page. See also this page for more tiling activities.]

Translation

Periodic tilings always include translations in more than one direction. Here is an example, using a basic brick layout:

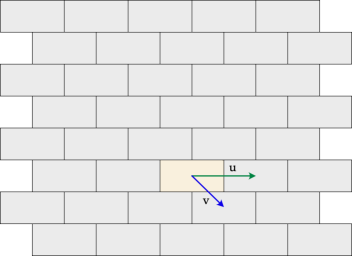
There are many options for translations that preserve the tiling. I chose two that connect the centers of bricks in such a way that you can get from any brick to any brick by combining translations using vectors u and v (or their opposites) repeatedly. For example, the top left brick in the figure can be translated to the bottom right using u + 7v. This provides a way to introduce vector addition.

Notice that from the point of view of symmetry, we are translating the whole tiling, but for our specific purpose of introducing translation and composition of translations to students, we are looking at individual tiles as pre-images and images (inputs and outputs).

Rotation

Periodic tilings may include centers of rotation. This example includes 2-way, 3-way, and 6-way centers:

Searching for rotation centers in a tiling is a good way to develop angle sense. Note that the only types of rotation that can be found in a periodic tiling are the ones in the above example, plus 4-way (90°) rotations. Here are two examples of tilings where one can search for centers of rotations:

In Islamic art:

In Escher prints:

[See also my pattern blocks wallpapers catalog.]

Composition of Two Half-Turns

2-way (180°) rotations are also known as reflections around a point or half-turns. An interesting theorem about half-turns is illustrated in any tilings that include them, such as the blue and green one above. In the fragment below, if you reflect the leftmost tile around O, the image is the middle tile. Reflect that around P, and you get the rightmost tile:

Theorem: The composition of the half-turns around O and P is a translation, parallel to the line OP, with length 2OP.

This can readily be proved using Euclidean geometry by following what happens to each point. It can be verified in any tiling that features 2-way rotations.

Reflection

Some periodic tilings feature lines of reflection (mirror lines). For example, the brick pattern includes horizontal and vertical mirrors through the center of the bricks. Two of those mirrors are shown here with dotted lines:

Note that the vertical mirrors also pass between bricks in every other row, while the horizontal mirrors do not.

The Islamic pattern mentioned above has horizontal, vertical, and also 45° mirror lines, passing through the centers of the brown octagons and the red 8-pointed stars. Some are shown in the figure:

To get a better sense of how reflections work, it is helpful to look at examples that contain asymmetric tiles, such as this one:

Each tile is an L Tetris piece. but you can also think of this tiling as made up of four-piece crosses, or two-piece rectangles. Some of the rectangles (blue and green) consist of an L and an upside-down L. The others (pink and orange) consist of a backwards-L, and an upside-down backwards-L. The L and the backwards-L are said to have different orientation. Within each (small) rectangle, the tiles have the same orientation, and are each other’s images in a half-turn.

The mirrors are the lines between the rectangles. On either side of each mirror, an L tile is reflected into a backwards-L, and vice versa. 

Composition of Two Reflections

In the above figure, start with a tile, perhaps the orange one at the top left. This will be our pre-image. Choose two parallel lines, horizontal or vertical. Reflect the pre-image in one line, and then reflect the image in the other line. No matter which two parallel lines you picked (and assuming the tiling goes on infinitely in all directions) the final image is another orange tile. You can get from the pre-image to the final image with a translation. How is the translation related to the two lines you chose? (Direction? Magnitude?) Confirm this by seeing what happens with other pre-images and the same lines. Try again with different parallel lines.

Theorem: The composite of two reflections in parallel lines is a translation perpendicular to the lines, in the direction from the first line to the second, and with magnitude equal to twice the distance between the lines.

Repeat this experiment, but this time use perpendicular lines. This time, if your original is orange, the final image is pink. Analyzing what happened should lead you to this conclusion:

Theorem: The composite of two reflections in perpendicular lines is a half-turn around their intersection.

Again, these theorems can be proven with basic Euclidean geometry, and verified on any tiling that has the needed mirror lines. 

Note that each reflection changes the orientation of the figure, so that after two reflections, we’re back to the original orientation. Indeed, unlike reflection, translation and rotation do preserve orientation.

You may be wondering what happens when you reflect in two lines that are neither parallel nor perpendicular. Here is an example:

Three mirror are shown with red lines. Choose two lines, and one tile to use as your pre-image. (It is easiest to see what happens if you choose a tile that touches the lines’ intersection.) Reflect your tile in one line, and its image in the other line. How can you get from the pre-image to the final image in one move? Yes, it is a rotation. Where is the center? What is the angle? How is it related to the angle between the mirrors?

Theorem: The composite of two reflections in intersecting lines is a rotation around the intersection, with an angle equal to twice the angle between the lines.

Glide Reflection

The glide reflection is the composition of a translation and a reflection in a line parallel to the translation vector. If you’re not familiar with it, see this introduction. The glide reflection is important, in part, because of this:

Theorem: Given two congruent figures a and b in the plane, if b is not the image of a in a reflection, translation, or rotation, then it is its image in a glide reflection.

(See the epic proof, illustrated with dynamic GeoGebra figures, on my website.) 

The glide reflection is essential in analyzing the symmetries of tilings (and any frieze or wallpaper designs.) Consider this tiling:

Choose one L (orange) and one backwards-L (green). They are clearly congruent, but there is no reflection, rotation, or translation taking one to the other. The relationship is a glide reflection. It is easiest to find the reflection line and translation vector in the case of adjacent figures, but they can be found for any such pair. The glide reflection lines are vertical, half-way between the blue squares.

Implementation

I hope this post convinced you that tilings can provide a useful context to teach many basic ideas about isometries (rigid motions). Certainly these suggestions do not constitute a full curriculum unit, but they can enrich any other approach. Do take a look at my Geometric Transformations page for other materials on this subject, some geared to grades 8-10, some for grades 11-12, and some possibly of interest to you as a teacher. I link to other related topics on my Symmetry page and of course on my Tiling page.

Finally, another ingredient in a well-rounded program on transformation basics is the use of GeoGebra or other interactive geometry software, as it makes it possible to experience transformations in a dynamic environment. But that’s the topic for another post.